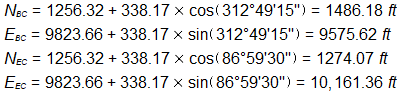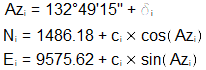Solution: Horizontal Curves Set 2
Problem (1)
Given the following information:
Δ = 45°49'45"
D = 07°09'43.1"
L = 693.90 ft
T = 338.17 ft
LC = 622.97 ft
D = 07°09'43.1"
L = 693.90 ft
T = 338.17 ft
LC = 622.97 ft
Curve Table
| Station | di, ft | δi | ci, ft | ||||
| EC Back | 57+24.88 | 639.90 | = L | 24°54'52" | = Δ/2 | 622.97 | = LC |
| 57+00 | 615.20 | 22°01'26" | 599.99 | ||||
| 56+00 | 515.02 | 18°26'34" | 506.18 | ||||
| 55+00 | 415.02 | 14°51'43" | 410.38 | ||||
| 54+00 | 315.02 | 11°16'51" | 312.99 | ||||
| 53+00 | 215.02 | 7°42'00" | 214.38 | ||||
| 52+00 | 115.02 | 4°07'08" | 114.92 | ||||
| 51+00 | 15.02 | 0°32'17" | 15.02 | ||||
| BC | 50+84.98 | 0.000 | 0°00'00" | 0.000 |
Determine curve point coordinates.
Compute azimuth of incoming tangent
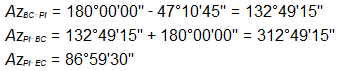
Compute coordinates of BC and EC
Set up the azimuth and coordinates equations
Using the az and coord equations, step through the table for each curve point
| Station | Azi | Ni, ft | Ei, ft | |||
| EC Back | 57+24.88 | 107°54'23" | 1274.07 | check | 10,161.38 | check |
| 57+00 | 110°47'26" | 1273.15 | 10,136.51 | |||
| 56+00 | 114°22'40" | 1277.25 | 10,036.66 | |||
| 55+00 | 117°57'32" | 1293.78 | 9,938.10 | |||
| 54+00 | 121°32'24" | 1322.46 | 9,842.37 | |||
| 53+00 | 125°07'15" | 1362.85 | 9,750.96 | |||
| 52+00 | 128°46'07" | 1414.32 | 9,665.30 | |||
| 51+00 | 132°16'58" | 1476.07 | 9586.73 | |||
| BC | 50+84.98 | 132°49'15" | 1486.18 | 9,575.62 |
Problem (2)
For the following short alignment data:
What are the coordinates of curve station 20+00.00?
Partial answers - computations are left to the reader.
NPI = 1151.53 ft
EPI = 1131.30 ft
NBC = 1052.74 ft
EBC = 589.35 ft
δ20+00 = 14°07'03"
c20+00 = 698.76 ft
Az20+00 = 93°47'13"
N20+00 = 1006.59 ft
E20+00 = 1286.58 ft