Solution: Traverse Area
Problem (2)
The owner of the parcel shown below hired a surveyor to determine the parcel area.
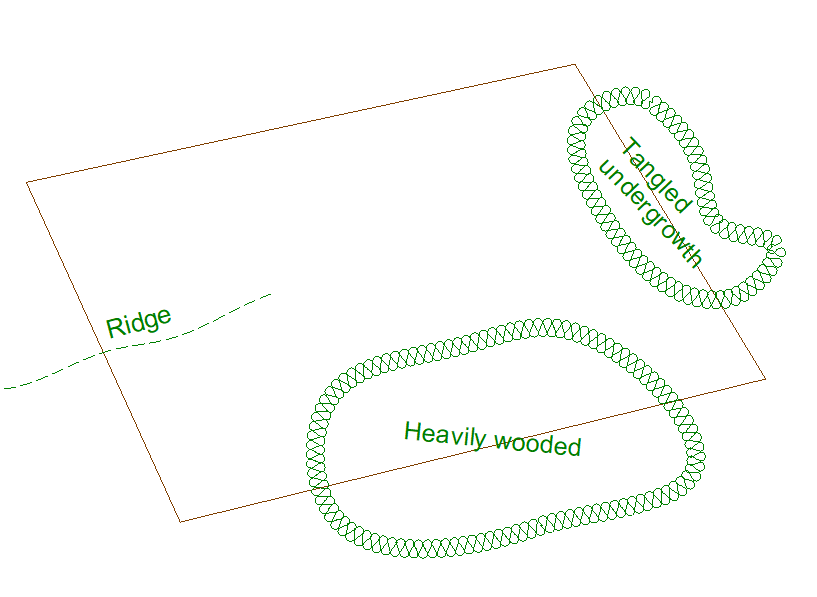
The surveyor was unable to run a simple loop traverse through the four property corners due to various obstructions. Instead, she created and measured a crossing-loop traverse (shown in blue). In addition to the parcel corners, additional points were needed to work the traverse around the obstructions.
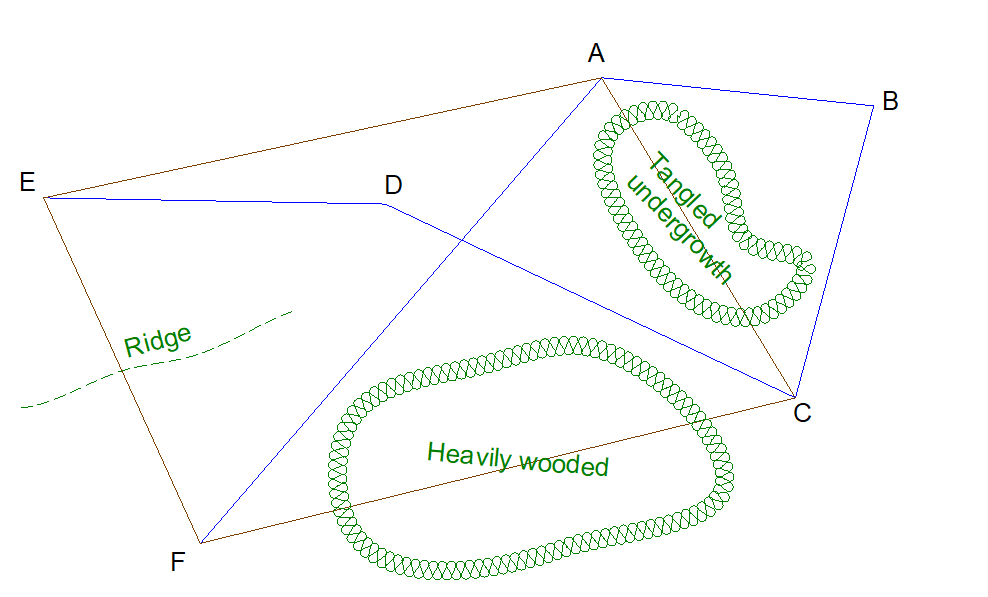
Reducing the field measurements resulted in a 1/17,300 traverse precision.The traverse was adjusted by the Compass Rule and coordinates were computed.
| Point | North (ft) | East (ft) |
| A | 600.000 | 1,000.000 |
| B | 569.612 | 1,293.788 |
| C | 254.542 | 1,209.288 |
| D | 463.631 | 766.846 |
| E | 470.303 | 397.969 |
| F | 97.543 | 566.876 |
What is the area and its expected error?
Answer
Arrange the parcel corner coordinates in order going around the parcel. Repeat the first corner at the end of the list. Use only points which which are parcel corners.
Cross-multiply and sum.
This solution starts at point A and travels clockwise around the parcel.
| Point | North (ft) | East (ft) | ||
| A | 600.000 | 1,000.000 | 254,542 | |
| C | 254.542 | 1,209.288 | 117,960 | 725,573 |
| F | 97.543 | 566.876 | 266,603 | 144,294 |
| E | 470.303 | 397.969 | 238,781 | 38,819 |
| A | 600.000 | 1,000.000 | 470,303 | |
| sums: | 877,890 | 1,378,989 |
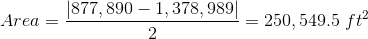
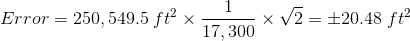
If you use sig fig and assume an additional digit was carried computing coordinates, then area should be statewd to 4-5 sig fig. If we use 5 sig fig, area would be 250,550 ft2 and the error would be a compatible ±20 ft2.
Area = 250,550 ft2 ±20 ft2